摘要:根据提供的信息,"x-1的展开"可能指的是数学中对表达式x减去1进行展开或运算的过程。具体展开的方式和结果取决于上下文和具体的数学运算规则。如需更详细或准确的解释,请提供更多背景信息或上下文。
本文将详细介绍关于X-1展开的各个方面,帮助读者更好地理解这一数学概念,我们将探讨X-1展开的定义、应用场景、步骤与方法、实例解析以及注意事项。
什么是X-1展开?
X-1展开是对形如X-1的表达式进行展开操作,在代数式中,我们常常需要对表达式进行化简、合并同类项等操作,而X-1展开是其中一种常见的操作方式,通过对X-1进行展开,我们可以得到一系列与X有关的项,进而进行进一步的数学运算。
X-1展开的应用场景
1、代数运算:在求解一元二次方程时,我们可能会遇到需要X-1展开的情况。
2、微分与积分:在微积分领域,X-1展开有助于求解函数的导数或积分。
3、几何与三角函数:在处理与圆有关的问题时,X-1展开有助于更好地理解和解决问题。
X-1展开的步骤与方法
1、识别表达式:识别出需要展开的X-1表达式。
2、展开操作:根据表达式的形式,对X-1进行展开,得到与X有关的各项。
3、化简与合并:在展开后,进一步对表达式进行化简和合并同类项。
不同类型的X-1展开的实例解析
1、线性表达式的X-1展开:(X-1)^2 = X^2 - 2X + 1。
2、二次表达式的X-1展开:(X-1)^n的二次表达式需要根据二项式定理进行展开。
3、含有其他变量的复杂表达式的X-1展开:(X-a)(X+b) = X^2 + (b-a)X - ab。
注意事项
在进行X-1展开时,需要注意以下几点:
1、确保需要展开的表达式是正确的,避免误判导致错误的展开结果。
2、遵循代数规则,确保每一步操作都是正确的。
3、在展开后,注意对表达式进行化简和合并同类项。
本文详细介绍了关于X-1展开的各个方面,包括定义、应用场景、步骤与方法、实例解析以及注意事项,通过本文的学习,读者可以更好地理解X-1展开这一数学概念,为后续的数学学习打下坚实的基础,希望本文能对读者有所帮助,如有不足之处,敬请指正,如需进一步了解和学习相关内容,可查阅相关教材或在线资源。
转载请注明来自河南军鑫彩钢钢结构有限公司,本文标题:《X-1展开式详解》



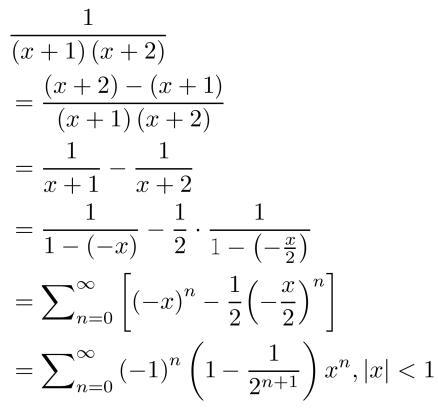
 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号
还没有评论,来说两句吧...